平板翼の揚力、モーメントの大きさと風圧中心位置は、飛行機の設計における基礎知識です。結論だけでも、勉強してください。平板翼の風洞実験結果はこの理論で始めて解明されています。また、回転モーメントの発生や紙飛行機の縦安定のページもこの理論の結果が使われています。

風圧中心：（ふつうは翼の）全空気力をその一点で支えることができる点
空力中心：（ふつうは翼の）全空気力によるモーメントが迎角によって変化しない点。
翼の場合，その翼断面形に関わらず，必ず前縁から翼弦長の25%付近の点に存在する

流れの中におかれた翼形に働く揚力も，後縁での流れを滑らかにするように境界層がはがれ，反時計まわりの循環Γをもった渦が放出されて流されていき，翼のまわりには時計まわりの強さΓの循環が残るためと解釈できる。速度Uの定常な流れで，揚力の大きさが流体の密度をρとするとき，ρUΓ に等しいというのがクッタ=ジューコフスキーの定理である
ここでΓは翼型を含む任意の閉曲線に沿って流速を線積分して得られる循環を意味する。これは、クッタが自分の1902年の論文中に埋もれていた関係式として1910年の論文で導いた式でもある。そのため、この式をクッタ・ジューコフスキーの定理と言う。
この式の見た目の簡単さとは裏腹に、ある流速Ｕの中に迎え角αで置かれた任意の翼型の循環Γを計算することは簡単ではありません。クッタやジューコフスキーは複素関数論の等角写像のテクニックを用いて、循環Γと翼型とを関係づける計算方法を開発して、低速・非圧縮生・完全流体における二次元翼設計法を確立した。

クッタ・ジューコフスキーの定理によると、一様流中におかれた物体に循環Γが付随していると、その物体には一様流に垂直な方向［紙飛行機では翼の上向き］に
揚力 = L = ρ U Γ
の力が発生する。
平板翼について複素関数理論を適用することで、循環Γの値を求めて次式を得る。

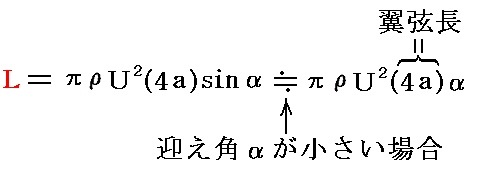
定理
空気流に対し平板翼を傾ければ揚力が、発生する。その大きさは、仰角、空気密度、翼弦長及び流速の2乗に比例する

平板を傾ければ、流れが非対称になり、翼周りに循環が付随せざるを得なくなり、それが揚力を発生させるのです。

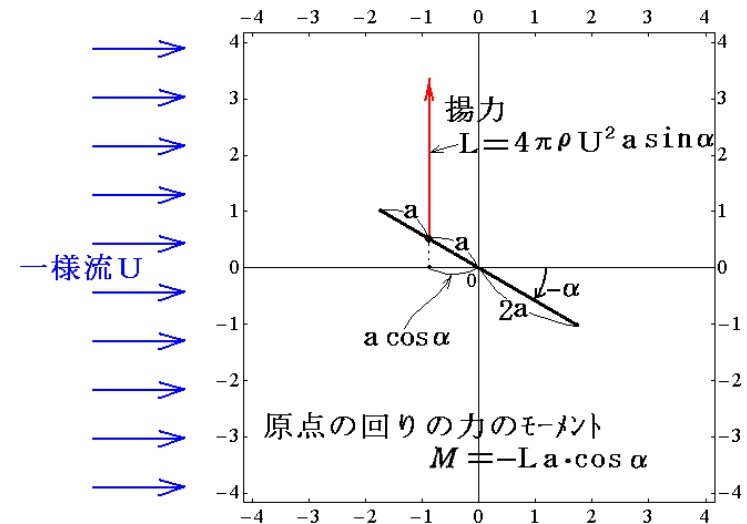
平板翼に働く圧力の合力複素速度ポテンシャルを用いて計算することで、揚力とその働く位置を計算できる。

定理
揚力の合力が働く位置［圧力中心］は平板翼の場合前縁から翼弦の1/4の距離の所にあることになる。また、原点周りの回転モーメントが発生し、その大きさは揚力と仰角に比例する。

参考 非圧縮性流体力学

平板翼の揚力、モーメント、空力中心

平板翼の揚力

平板翼のモーメント

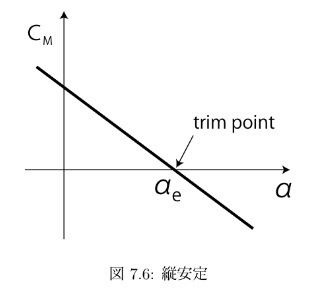
縦の安定