WEBの世界の基本構造について、知ることは　ネットのビジネスを考える場合、避けて通れない。
基本構造の不変性について市川惇信先生の「狭い世の中」　をみて啓発されました。

　WEBは、スケールフリーのネットワーク構造(Scale Free Network)を持つ。ここは、狭い世間と言って良い。
1999年のBarabasiらの研究とその後の事例研究で明らかとなった。
　WWW の地図を作成する際にその度数分布が釣鐘型のランダムネットワークのものと一致しないことを発見した。
・80％以上のページはリンク数が4未満であるが、0.01％未満のページは1,000以上のリンク数であることがわかった。
・あるノードがk個のリンク数を持つ確率は1/kn（nは約2）に比例しており、その分布は「べき乗則」とよばれる。
・べき乗則に従う場合、少数のリンクを持つ大多数のノードと、非常に多くのリンク数を持つごく少数のノード（「ハブ」と呼ばれる）が存在する。
・ランダムネットワークの度数分布は平均から大きく外れるほどノード数が少なくなる。このことは、系を特徴づける「スケール（尺度）」が存在すると表現される。

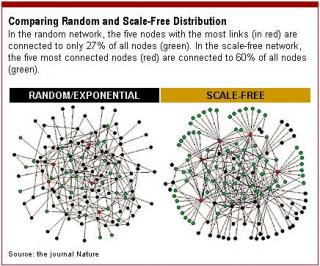
スケールフリーとは
べき乗則に従うネットワークでは、そのようなスケールが存在しない（フリーである）。近年、スケールフリーネットワークの実例が数多く見つけられてきた。
判り易く言えば
-WWWの利用実態は、非常に大きいリンク数をもつ少数の巨大接点（ハブ）と殆どの少数リンクしかもたない節点からネットワークから成り立つ
-人間の身長分布のように、平均の周りに正規分布するような世界ではなく、少数の巨大と大多数の極小が存在する極めて特徴のある構造。
-これは、感染症の伝播ネット、物の売買ネット、生態系の食物連鎖などでも見られる

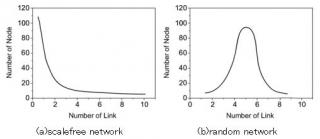
成長の原理
このような、構造は、Webのリンクとノード（HTTP）の成長の原理
１．成長(Growth)：自律的に新たな節点が追加され続ける。ネットワークは1度に１つだけ節点を増やす。
２．優先接続(Preferential Attachment)：新しい辺はより多くの辺を持つ節点に結合しやすい。すなわち、ある節点が選択される確率は、その節点がすでに獲得している辺数kに比例する。
この原理に従って、成長を繰り返し続ければ、実現されることがわかっている。
　言い換えれば、ひとたびこの構造が生育すれば、構造改革はよほどの規制か破壊的転換をしないと、構造は変わらないということになる。
多くの客を集める巨大ASPが安心しそうな話題になってしまった。
都市構造の改革との対比
昔、全国総合計画で政府は中核都市（幕張や大宮など）を育成し、多核多心型都市構造を実現しようとした。方策は環状道路網や鉄道網の形成、業務核地域の開発などであった。
当時の努力で多少は、立地したが、構造変化までは起きていないという評価が妥当であろう。
ここでも、都市の成長の原理が研究されていた。
１．都心に勤務するために、人は、限られた時間の制約のもとで、出来るだけ交通コストが少ないところを選択し立地する
２．併せて限られた所得の制約のもとで、一定規模の住宅を確保しようとする。
この原理だけで、都市を成長させれば。
結論として、人口密度は都心を最大とする指数分布に従う。
現実に、東京の鉄道沿線の人口密度は指数状の分布となっている。
　都市の基本構造は、１．２．の経済行動に変化なければかわらないということになる。
　リアルな住宅立地の世界では、土地利用や交通などの制約が多いが、WEBネットの世界は、規制が少ないので、とてもわかり易い構造が出現する。
発見事例１：Mixiのリンク構造ソーシャル・ネットワーク・サービスで有名なMixiは、友達の輪をもつサービスであるが、ここの仲間のリック構造は、まさにべき乗則であった。http://www.itmedia.co.jp/news/articles/0509/14/news040.html
発見事例２：P2Pのネットワーク
ファイル交換などP2Pの交換状況をトレースした結果が報告されている。そのネットワークの図はまさに、スケール　フリー　ネットワークであった。
P2Pネットワークの図
この構造のもつもう一つの特徴が、「狭い世間」である。
ｋ回のファイル交換で届けることのできるノード（PCまたは人）の数は膨大である。5回も繰り返せば、世間中に情報が届いてしまうような、「狭い世間」の構造をもっている。人気さえあれば、一瞬で世界に配布（自律的に）されるということ。
　これは、DELLのPCが普及したり、ipodが普及したりする上の需要側の構造であり、グローバルに売れる商品をもつ企業が、世界を制覇し巨大企業となる構図でもある。ファミコンがセガを打ち負かした構図でもある。（セガの場合は生産面でも、コストのどんどん低下する汎用PCパーツを採用しなかったので、不利になったと聞いている。）
　最近は、世界中に部品を販売するトップ企業が好調かつシェアが高まる一方で、総合的大手組立メーカー（例えば家電製品など）が不調なのも、この需要構造で説明できる部分が多々ある。
　私の好きな釣りの世界でもガイドのメーカーの富士工業やリールのシマノなど、世界に売って、元気で嬉しい。
　ものづくりでは、元気な企業が多いが　ITの関連分野では　日本の企業は精彩がなくなっている。元気なのはキャノンやシャープなどであり、肝心のソフトは振るわない。カーナビを世界に売ってほしいと願っていたが、GoogleMap　やGoogleAPI　の今日この頃をみると、日本のカーナビとマッピングソフトに対して悲観的になってしまう。
「狭い世間（ネット社会）の渡りかた」
１．グローバルに売れる小物（ものやソフト）を創造すること
　　そしてstrategicの根気よく育てること（検索でスタートしたベンチャーGoogleのように)
３．国内の規制や特種な調達に頼らないこと
４．最終の組立ては、グローバルな差別化あっての組立て
５．戦略無き戦術論議に時間をかけず、戦術無き戦闘にリソースを消耗させないこと
などなど
コミュニケーションから見た組織論
　Barabasiの研究から、一定回数の連絡や相談や会議で、一挙にコミュニケーションができるような組織構造がわかる。これは、確定的なスケールフリー（Deterministic Scale Free Network)の構造である。
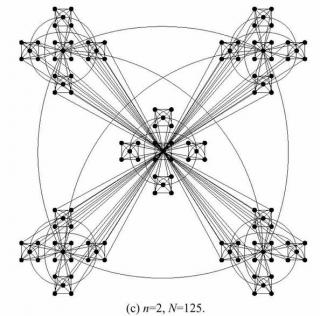
　最適なFlowの構造を、125人（ノード）の場合で表現すれば
下記のようになる。
　これは、コミュニケーションが重要な産業（例えば、研究所、コンサルタント、ソフト開発など）ひとが創造するもので生きている会社（創造体）にたいする知見であろう。
　とても、Simpleできれいな、自己相似形である。（フラクタル図形の教訓と呼びたい）
フラクタル図形の教訓：純創造体の組織
１．5人組の創造体を重視し、最小単位とする
２．階層階を重ねないこと（承認プロセスの最短化）
３．縦のコミュニケーションより横のコミュニケーション重視
４．中央に会議やWebを設け、情報共有の場（リーダーシップ/巨大サイト）を設ける
世の中に、純創造体は有り得ないので、このバリエーションとなる。
軍隊のような機能体は、これをまねしないこと。（創造不要のマニュアル通り実行する戦闘集団の場合は、逆効果になる）

ここで問題提起
（問題１）
ノードに能力差があった場合の創造体組織の最適な構成はどうなるか。
古くから、人材配置の集中と分散について、考えが対立している。
１．優秀な人材を弱体（成長の遅い）な部署に移動し分散させる一方、能力の低い人材も分散させる。（分散/分散方策）
２．優秀な人材を集中させると同時に能力の低い人材も集中させる。
３．優秀な人材は、集中。極度に低い人材は分散。
４．極めて優秀な人材は分散。能力の低い人材は分散
５．上記のような、介入をせず成長に任せる
以上の４つの配置方法のいずれがより成長する組織となるか。
ただし、組織全体の専門性は、おおきく変わらないとする。
（問題２）
また、部署毎に専門性が異なり、他の部署に移動した場合蓄積に時間がかかる場合はどうか。異分野の専門がシナジーを生むか否か。あるいは、専門性をどのように分類するかが問われるので、さらに難問となりそう。
（問題３）
　ものづくりでなく、事づくりの世界（ソフトや開発研究）では、優秀な人材が集中、あるいは輩出する組織が現れ、成長を生み出すケースが多いが何故か。（ある水準を越えた差別化できる知見しかビジネスにつながらないような分野での、人材配置の最適性の研究はあるか。）
人の能力の市場価値は、その身長のように正規分布をしているか。残念ながら、現実の論文の参照（リンク）でみたネットワーク構造は、スケールフリーであるといわれている。大量に参照される知の巨人から多くの凡人まで、べき乗則で分布している（能力の市場価値の偏在）ならば、どのような組織成長戦略がありうるか。
これは、英才教育の重要性（長らく否定されてきた。劣後者に合わせることで全体が引きずられない教育）が再認識されなければいけない話になりそうである。
　知性とはなにか、脳の研究をひも解く必要がある話となってきた。知性の内、よく観る、正しく見えるということは、それぞれの領域で観続けないと備わらことが知られている。釣りの例でも、島の子供たちは、海の魚の動向がよく観える。知性の基本は、言語認識がそうであるように、習うより慣れろ、そして知覚せよということが基本にあるようだ。見えるまでに、何年かかかり、また、ひとがどの動物よりも、教育期間が長いのからみても、そのようだ。
2005年9月　　　　　　　　　　　　　　　　　　　　　　　　　　　青海波亭　IT_随想
参考用:日本語のしっかりしたサーベイ研究がみあらたない
１．Barabasiの研究などいろいろ要約
２．．少年老い易く学成り難し：数学・確率など動向など紹介：素晴らしいサイト